Last updated: 30/09/2017, 2 min read
Total pressure losses
The total pressure loss (ΔP) in a pipe/tube or duct system can be expressed by the following equation:
ΔPl: linear pressure losses (in the tubes)
ΔPf: pressure losses in pipe fittings (elbows, tees, etc.)
ΔPv: pressure losses in the control valves
I consider the control valves as essential part of piping systems, that’s why I exclude them from the general fittings category. Furthermore, in some heating systems, the adjustment of control valves can result in a desired/predetermined value of the system’s pressure losses, which in many cases is almost equally important to the flow regulation.
Linear pressure losses
The linear pressure losses are calculated by the following equations:
ΔPl: linear pressure losses [Pa]
ρ: fluid density [Kg/m³]
g: acceleration due to gravity [m/s²]
hf: head losses [m]
f: friction factor [-]
L: pipe length [m]
D: pipe internal diameter [m]
V: average fluid velocity at the cross section [m/s]
The second equation is widely known as Darcy & Weisbach’s equation. In the previous post, you can find over 10 ways to calculate these losses.
Pressure losses in pipe fittings
Fitting losses – sometimes in the literature are referred to as local or minor pressure losses – are usually expressed as a function of the velocity head (v2/2g):
Where:
ΔPf: pressure losses in pipe fittings [Pa]
ρ: fluid density [Kg/m³]
ΣK: total resistance coefficient of pipe fittings [-]
V: average fluid velocity at the cross section [m/s]
Each type of fitting has a resistance coefficient that is found experimentally. In most cases, these factors can be found in the literature (see Crane for example). Some typical values are given below:
- Tee, flanged, line flow 0.2
- Tee, flanged, branched flow 1.0
- Elbow, threaded regular 90º 1.5
- Elbow, threaded regular 45º 0.4
- Return bend, threaded 180º 1.5
- Water meter 7.0
Pressure losses in control valves
The pressure losses in control valves can be expressed by the following equation:
Where:
ΔPv: pressure losses in the control valve [Pa]
SG: specific gravity of the fluid (= ρ/ρwater) [-]
Q: flow discharge {m³/h]
Kv: control valve flow coefficient [m³/h/Pa, although it is usually expressed in m³/h/bar or in m³/h/KPa]
The flow coefficient can be found from the control valve’s manufacturer. This factor is typically given in diagrams that have flow on one axis and pressure drop on the other. A typical example for a water valve is provided below (taken from Spirax/Sarco).
Note that in many cases a conversion between units is required to be compatible with the above equations (i.e., bar to Pa, l/h to m³/h, etc.). However, in an older post, you can find a useful
units converter.

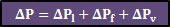

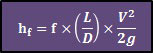
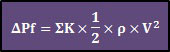
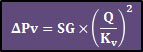



Συγχαρητήρια για την δουλειά σου.Σε παρακαλώ όμως να διορθώσεις τον τύπο ΔΡΙ= ρ x Hf Με τον σωστό ΔΡΙ = ρ x g x Hf
Basilhat, σε ευχαριστώ πάρα πολύ για τα καλά σου λόγια, καθώς και για την παρατήρησή σου. Είχες δίκιο φυσικά για τον τύπο, τον οποίο τον διορθωσα.
Για αποφυγή παρεξηγήσεων/μπερδεμάτων πρόσθεσα και τις μονάδες δίπλα..
Σε ευχαριστώ και πάλι!
Συγνώμη αλλά δεν καταχωρήθηκε και στο ξαναποστάρω.
ΔPΙ = ρ x g x Hf αντί του ΔΡΙ = ρ x Hf που γράφεις στο άρθρο σου.
Είμαι ο Basilhat απο το γνωστό φόρουμ.Απο εκεί βρήκα και την ιστοσελίδα σου την οποία βρήκα πολύ ενδιαφέρουσα.Διαβάζοντας το συγκεκριμένο άρθρο έπεσε το μάτι μου στο λαθάκι που σου πόσταρα παραπάνω ως ανώνυμος.