Definition
Creep is the tendency of a solid material to slowly move or deform permanently under the influence of constant stresses and constant temperature. It occurs as a result of long term exposure to levels of stress that are below the yield strength of the material. These stresses and temperatures cause the mobility of dislocations and discontinuities in the material, which is the main reason of creep development. At elevated temperatures, this process is more severe resulting in a degradation of material’s performance.
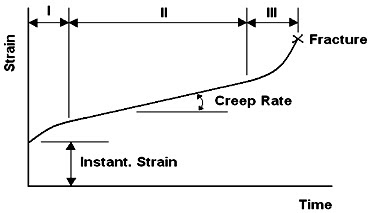
Figure 1: Typical creep curve [1].
In the above figure is shown a generally accepted idealization of the creep process. Creep is considered as a four-stage process:
- The first stage (elastic stage) involves an initial strain, namely a pure elastic deformation.
- The second stage is called primary creep. It is the predominant stage at low stress and temperature levels (i.e. room temperature). Material’s creep resistance is increased as a function of its own deformation.
- The third stage is named secondary creep. Here the creep rate is constant and minimum (due to the balance between the competing processes of strain, hardening and recovery) and it is the most desirable stage
- The last stage is called tertiary creep. It is an unreal situation that occurs at high stress and temperature. There is a significant reduction in the cross sectional area, as well as metallurgical changes (i.e. recrystallisation).
Creep can appear even at low temperatures (below the half of the melting temperature), but for most of the constructional materials it will be insignificant. The creep damage can take several forms. For instance, the simple creep deformation can lead to dimensional changes that result in distortions, loss of clearance, wall thinning etc.
Creep analysis
Most of the materials used in turbomachinery are susceptible to creep. Creep is a function of stress, temperature, strain and time. Since it is very complex to be defined, the common method of representing creep data is by using materials’ tables. In these tables, the minimum creep stress that causes a plastic strain of a certain percentage of the total plastic strain in a certain amount of time is represented (i.e. 0.1% total plastic strain in 10000 hours for an industrial gas turbine).
The prediction of failure time under the combination of different stress and temperature is done by using an extrapolation method. In this method, short term creep tests are performed and the creep rate is calculated. Then, it is assumed that this creep rate remains constant throughout the lifetime of the component.
A common method of extrapolation from short times to long times, is to use a relationship that describes the creep strain in as a function of stress and temperature. This relationship will include the so-called “time-temperature parameters”, in which is assumed that time and temperature are conversely proportional. This means that an increment in operating temperature will result in a reduction in the time needed to reach a particular creep state and vice versa. The above assumption is true only if one reaction control the process over the entire temperature range.
The most common time-temperature parameter is known as the Larson-Miller parameter. It is derived from an Arrhenius-type equation, which determines the creep rate as a function of temperature and stress:

Where Q is the activation energy for creep, R is the universal constant of gases, T is the absolute temperature, A and n are constants, and σ is the stress. The three constants, A Q and n, are determined experimentally and are depended on the material. The creep rate is exponentially depended on temperature. A 20°C increase in temperature results in an almost double creep rate. If the above relationship is rewritten using logarithms, it gives the Larson-Miller parameter:

Where T is the absolute operating temperature in K, t
r is the time to rupture in hours and C is a constant (between 15 and 30). The value of constant C is obtained graphically from the interception of log
10tr, when is plotted against 1/T. For the most industrial applications it is considered equal to 20.
A typical operating cycle of an industrial gas turbine can be divided into three sections: start-up, operation and shutdown. Each section has different operating conditions that imply different stresses and temperatures. In order to add the effects of each section, the Miner’s Law is used:

The Miner’s law is an inverse sum law, which states that the sum of life fractions must be unity. By using the Larson-Miller parameter the time to failure for each section can be determined. Hence, if the real time spent at each section is divided by the total time to failure, the life fraction can be found. Then, by using Miner’s law, the sum of all life fractions should be unity. The Miner’s law make use of a linear damage sum assumption, in which the damage to each operating section is related with the ratio between time spent and time to failure. Furthermore, it assumes that the component’s failure will take place when the sum becomes equal to unity. As matter of fact, failure occurs when the sum is somewhere between 0.7 and 1.4.

Figure 2: Larson-Miller parameter versus stress to rupture for austenitic stainless steel [1].
It should be highlighted that the Larson-Miller method is not a fully proved method. This means that attention should be paid when extrapolation is used into high temperature field, because metallurgical changes may occur and the material will be completely different.
Another point that needs attention is the Larson-Miller parameter approach, which is based on curves that are known as Larson-Miller creep curves. The problem is that these curves are based on rapture, and consequently, the estimated total creep life is referred to the rapture of the blades. Nevertheless, the HPT components (the disc and the blades), before they reach that critical condition, are subjected to a progressive creep deformation that damages the casing (notably via scraping) and the HPT itself (the disc and the blades may stop working due to the excessive distortion). This problem is usually avoided by using a safety factor of about 2/3 (66%).
References
The article was based on my M.Sc. progress review:
Samaras C., 2009, “Emissions and lifetime estimation modeling of industrial gas turbines”, M.Sc. Progress Review, Cranfield University, UK.
The figures were found from:
[1] Suria ,O. V., 2006, “A flexible lifing model for gas turbines: Creep and low cycle fatigue approach”, M.Sc. Thesis, Cranfield University, U.K.
Read also
Fatigue Analysis In Turbomachinery
High Pressure Turbine: Stress Sources And Cooling