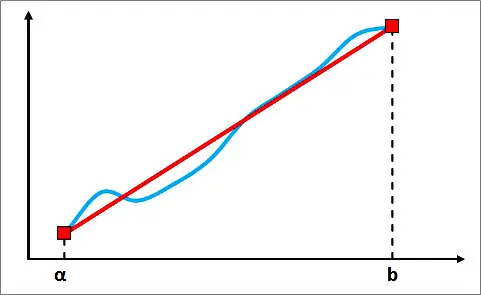
The basics
A common complaint about Excel is that it doesn’t directly calculate a function’s integral. If the function is represented as a curve in a chart, then the integral is defined as the (net signed) area under that curve. If you have to calculate the area under a curve, you must think of an indirect way to do it. One popular method for accomplishing this task is the so-called trapezoidal rule.
According to Wikipedia: “The trapezoidal rule is a technique for approximating the definite integral:
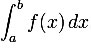
The trapezoidal rule works by approximating the region under the function f(x) graph as a trapezoid and calculating its area. It follows that:”
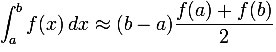
Calculate the area under a curve/the integral of a function
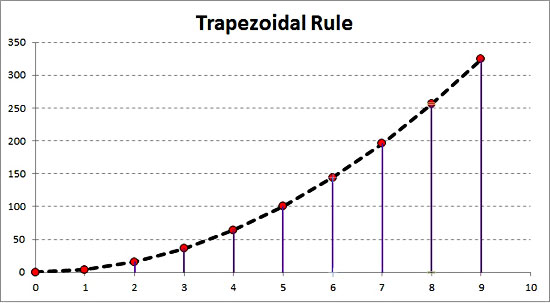
1st method: Spreadsheet calculations
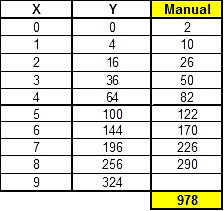
If n points (x, y) from the curve are known, you can apply the previous equation n-1 times and sum the results. For example, in the sample workbook, we had the function y = 4*x^2; we knew 10 points, so we applied the formula 9 times. For the first point the result was (1 – 0)*(4 + 0)/2 = 2, for the second (2 – 1)*(16 + 4)/2 = 10 and so on. The picture above contains the entire set of calculations.
2nd method: SUMPRODUCT formula
With this method, you avoid the intermediate calculations, and by using only one function, you get the result. However, the difficulty level is a little bit higher than the first method (especially if you are new to Excel). The method involves the SUMPRODUCT function, the syntax of which is given below:
SUMPRODUCT(array1, [array2], [array3], …)
The SUMPRODUCT function multiplies the corresponding components in the given arrays and returns the sum of these products. Array1, array2… are the ranges of cells or arrays that you wish to multiply. All arrays must have the same number of rows and columns, and you must enter at least 2 arrays (you can have up to 30 arrays).
The tricky part is the array/range definition. If n curve points (x, y) are known, the function can be written:
![]()
In the sample workbook, the SUMPRODUCT function is used with the following ranges:
=SUMPRODUCT(A5:A13-A4:A12;(B5:B13+B4:B12)/2).
In reality, we applied the same function as in method 1, but instead of single cells, we had multiple cells/arrays. The function performs the following calculation:
![]()
Without any doubt, the second method is much more straightforward than the first one.
3rd method: Custom VBA function
At your Excel file, switch to VBA editor (ALT + F11), go to the menu Insert Module and add the following code lines.
Option Explicit
Function CurveIntegration(KnownXs As Variant, KnownYs As Variant) As Variant
'---------------------------------------------------------------
'Calculates the area under a curve using the trapezoidal rule.
'KnownXs and KnownYs are the known (x, y) points of the curve.
'Written By: Christos Samaras
'Date: 12/06/2013
'Last Updated: 21/06/2020
'E-mail: [email protected]
'Site: https://myengineeringworld.net
'---------------------------------------------------------------
'Declaring the necessary variable.
Dim i As Integer
'Check if the X values belong to a range.
If Not TypeName(KnownXs) = "Range" Then
CurveIntegration = "Xs range is not valid"
Exit Function
End If
'Check if the Y values belong to a range.
If Not TypeName(KnownYs) = "Range" Then
CurveIntegration = "Ys range is not valid"
Exit Function
End If
'Check if the number of X values is equal to the number of Y values.
If KnownXs.Rows.Count <> KnownYs.Rows.Count Then
CurveIntegration = "Number of Xs <> Number of Ys"
Exit Function
End If
'Start with zero.
CurveIntegration = 0
'Loop through all the values.
For i = 1 To KnownXs.Rows.Count - 1
'Check for non-numeric values.
If IsNumeric(KnownXs.Cells(i)) = False Or IsNumeric(KnownXs.Cells(i + 1)) = False _
Or IsNumeric(KnownYs.Cells(i)) = False Or IsNumeric(KnownYs.Cells(i + 1)) = False Then
CurveIntegration = "Non-numeric value in the inputs"
Exit Function
End If
'Apply the trapezoid rule: (y(i+1) + y(i)) * (x(i+1) - x(i)) * 1/2.
'Use the absolute value in case of negative numbers.
CurveIntegration = CurveIntegration + Abs(0.5 * (KnownXs.Cells(i + 1, 1) _
- KnownXs.Cells(i, 1)) * (KnownYs.Cells(i, 1) + KnownYs.Cells(i + 1, 1)))
Next i
End Function The advantage of this custom function is that you don’t need to worry about the input ranges. The code checks if the x and y values are (valid) ranges and if the x and y ranges are equal (for example, if the input is 10 x values and 10 y values). If something goes wrong, the function returns an error message instead of the value. So, you only have to insert the input ranges in the function, and the function will return the curve area. In the sample workbook, for example, the custom function was used with the following ranges (we had 10 x values and 10 y values – 10 curve points):
= CurveIntegration(A4:A13;B4:B13)
Limitations of the trapezoidal rule
As highlighted in the beginning, the trapezoidal rule is an approximate method to calculate the area under a curve/perform numerical integration. In the sample workbook, you will notice that, for the particular curve, all 3 different ways that were described above result in the same value (978). You might believe that since the 3 methods agree on the final value, this is the correct one. Unfortunately, this is not true!
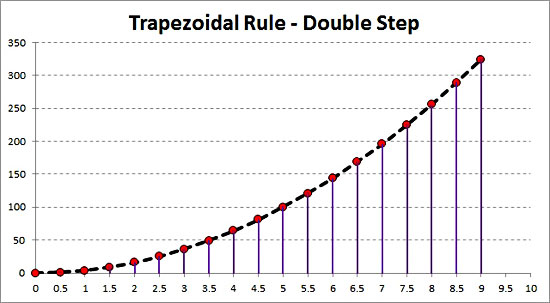
The accuracy of the trapezoidal rule is firmly related to the number of known curve points. The more points you know, the more the trapezoids, so the better the approximation (for a specific range). If in the specific example we knew 20 points (step 0.5) instead of 10 (step 1), then the result with 3 methods would be 973.5.
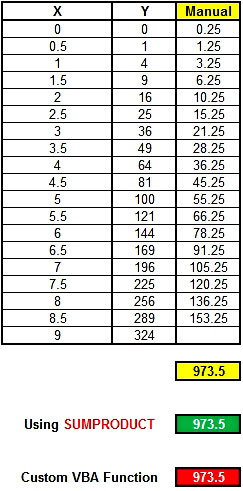
If we knew 901 points (step 0.01), the result would be around 972, which is the correct one. How do we know that 972 is the right one? The answer is simple: for the particular example, the curve was based on the function y = 4* x^2. For the x range 0 to 9, the integral of this function will be:
![]()
Although the trapezoidal rule is a simple way to calculate the area under a curve, you should never forget that it is an approximate method. The more points you have, the better the results you get. Furthermore, be careful not to confuse the curve area with the value of the definite integral. They are not the same since the area cannot be negative by definition!
When you use the trapezoidal rule to calculate a curve area, you have to be careful in cases where the curve is below the x or y-axis. If it is, you should use the abs function (returns the absolute value of a number) in the first two methods to get the correct area, while the custom VBA function has already implemented it.
Downloads
The file can be opened with Excel 2007 or newer. Please enable macros before using it.
Read also
Numerical Integration In Excel Using The Composite Simpson’s Rule
Calculating The Area Of A Simple Polygon Using The Shoelace Algorithm
Page last updated: 21/06/2020


Thank you for your kind words, Kwasi!
Indeed, students from several scientific fields might find this article useful.
The integral calculation is quite a common task, so by using Excel and any of the above methods you can get a relatively good approximate right away.
Best Regards,
Christos
the curve (AUC) determinations are really also in the health sciences (physiology, nutrition and chemistry etc.). Students in these areas will find this content highly useful.